text_test04.gp を使います。
まずはピークの位置がほかの成分から別れている
gnuplot は version 3.7 から、マルカール法を使った 非線型フィッティング が使えるようになりました。 詳細については文献 104に譲ります。
コマンドファイルとして、
text_test04.gp を使います。
まずはピークの位置がほかの成分から別れている
![]() Cs のスペクトルを見てみましょう。
230 ch. 辺りのピークはほとんど正規分布していますので、
Cs のスペクトルを見てみましょう。
230 ch. 辺りのピークはほとんど正規分布していますので、
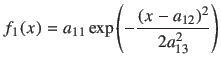 |
(1) |
f1(x) = a11*exp(-((x-a12)/a13)**2/2) a11 = 2000 ; a12 = 230 ; a13 = 10 fit [210:240] f1(x) "text_test04_cs137.dat" using 1:2:($2**0.5) via a11,a12,a13この部分のフィッティングの結果は次のようになります。
Final set of parameters Asymptotic Standard Error ======================= ========================== a11 = 1989.14 +/- 21.14 (1.063%) a12 = 225.805 +/- 0.06535 (0.02894%) a13 = 7.25809 +/- 0.06076 (0.8371%)このようにして、ピークの位置と高さ、幅の情報を得ることができます。 右に表示されているのは、それぞれのパラメータの決定精度(誤差)です。 フィッティングの結果は、
plot [0:300] f1(x), "text_test04_cs137.dat"とplot コマンドを用いて表示させます。
ところが、データによっては初期値を工夫してもうまくフィッテングできない場合があります。 これは、関数がデータと合っていない場合もありますが、パラメータの大きさが非常に違う場合にも起こります。 上の例では、a11とa13の比は300程度でした。この比が大きくなるとgnuplotは一方を0と判断してエラーを返すことがあります。 また、幅a13がピーク位置a12に比べて非常に小さい場合にも、フィッテングがうまくできない場合があります。 このようなときは、
f1(x) = a11*100*exp(-((x-a12-200)/a13)**2/2) a11 = 20 ; a12 = 30 ; a13 = 10 fit [210:240] f1(x) "text_test04_cs137.dat" using 1:2:($2**0.5) via a11,a12,a13のように、定数倍や定数値のオフセットをつけてa11,a12,a13の値を同じ桁にするとうまくいきます。
次にK-X 線のピークのフィットを試みましょう。 K-X 線のピークの部分には、 ほぼ一定の値を持つピーク成分以外の成分があります。 先ほどのような単純なGauss 関数ではなく、
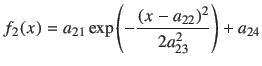 |
(2) |
f2(x) = a21*exp(-((x-a22)/a23)**2/2)+a24 a21 = 1400 ; a22 = 15 ; a23 = 3 ; a24 = 200 fit [10:16] f2(x) "text_test04_cs137.dat" using 1:2:($2**0.5) \ via a21,a22,a23,a24
次に![]() Co のスペクトルですが、2本のピークはお互いが
少なからず重なっており、さらに
コンプトン端と重なる部分もあり、
Co のスペクトルですが、2本のピークはお互いが
少なからず重なっており、さらに
コンプトン端と重なる部分もあり、
![]() Cs のスペクトルの時に比べると
初期値を与えることも簡単ではありません。
gnuplot では、定義した変数の値が保持されるので、
この特徴を活かして、順次初期値を変更しながら
フィッティングを実行してみましょう。
Cs のスペクトルの時に比べると
初期値を与えることも簡単ではありません。
gnuplot では、定義した変数の値が保持されるので、
この特徴を活かして、順次初期値を変更しながら
フィッティングを実行してみましょう。
まず、
ピークを2本のガウス分布で表現し、
コンプトン散乱等の成分を部分的に2次関数で表現することにしましょう。
![]() は 1.332 MeV のピーク、
は 1.332 MeV のピーク、
![]() は 1.173 MeV のピーク、
は 1.173 MeV のピーク、
![]() は コンプトン散乱等の成分として、
は コンプトン散乱等の成分として、
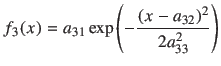 |
(3) | ||
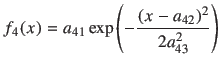 |
(4) | ||
| (5) |
| (6) |
まず、手順ですが、次のように考えてみました。
b1=0.01 ; b2 = 500 ; b3=1 #fit [320.0:360.0] g1(x) "text_test04_co60.dat" via b1, b2, b3のようにフィッティングの部分をコメントアウトして、 手作業での入力が初期値になるようにしましょう。
個別にフィッティングを行ったため、1.173 MeV のピークの部分が 過大に評価されている様子がわかります。
さて、これらの初期値を使って最終目標である全体のフィットを 行ってみましょう。 コマンドはかなり長くなりますが、次の通りです。
fit [300.0:500.0] h(x) "text_test04_co60.dat" using 1:2:(sqrt($2)) \ via a31,a32,a33,a41,a42,a43,b1,b2,b3 plot [200:550] h(x), f3(x),f4(x),g1l(x),\ "text_test04_co60.dat" using 1:2:($2**(0.5)) with yerrorbar結果は全体を示す関数
結果は図17の通りで、2つのピークの部分は 良く再現されています。 念のため書き加えますが、 フィッティングの結果はあくまで gnuplot の持つフィッティングルーチンの出した答えであって、 その妥当性は解析する人が考える必要があります。